对于极值调节控制对象,文献提出一种自适应动态寻优方法,它成功地解决了使用传统的动态寻优方法在实际工业生产过程中无法回避的一个难题,即保证极值调节控制系统运行的连续性和稳定性问题。因为若用传统的动态寻优方法,当极值调节控制对象的参数飘移后控制系统就不能正确地进行动态寻优,就必须把控制系统停下来重新辨识极值调节控制对象的参数,再重新整定控制系统的参数。而自适应动态寻优方法最突出的优点就是在动态寻优的过程中不仅能够自动辨识控制对象的参数,而且还能够自动适应参数的飘移,因此有效地保证了控制系统运行的连续性与稳定性。而且这种自适应动态寻优方法对极值调节控制对象的先验知识要求非常少,只要知道控制对象的阶数就能始终正确地进行动态寻优。其主要思想如下所述。
1 自适应动态寻优方法简要回顾
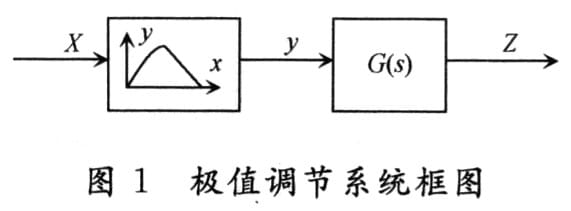
寻优系统采用步进式调节器,步进周期T0是固定的。极值调节对象可以分解为非线性环节与线性环节的串联,如图1所示。
设极值调节对象线性部分的传递函数为:
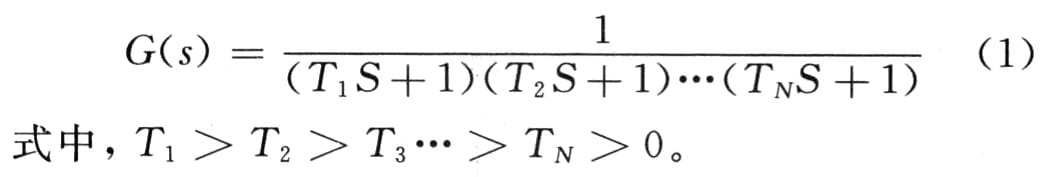
单位阶跃响应为:
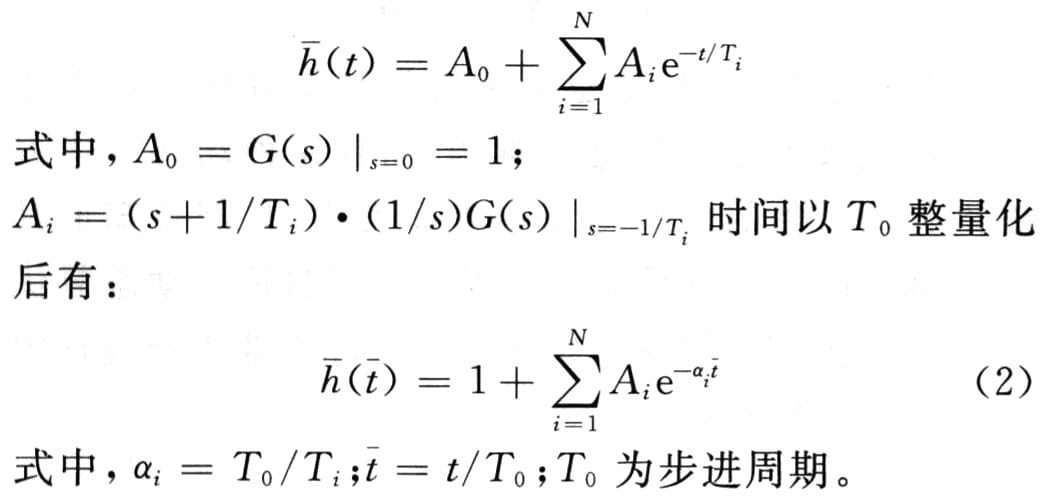
设系统的输出如图2所示,把每个步进周期分成相等的2N等份,在每个分划点进行采样并取2N+1个采样值,预估比较点在试探步后的第一个采样点上进行。
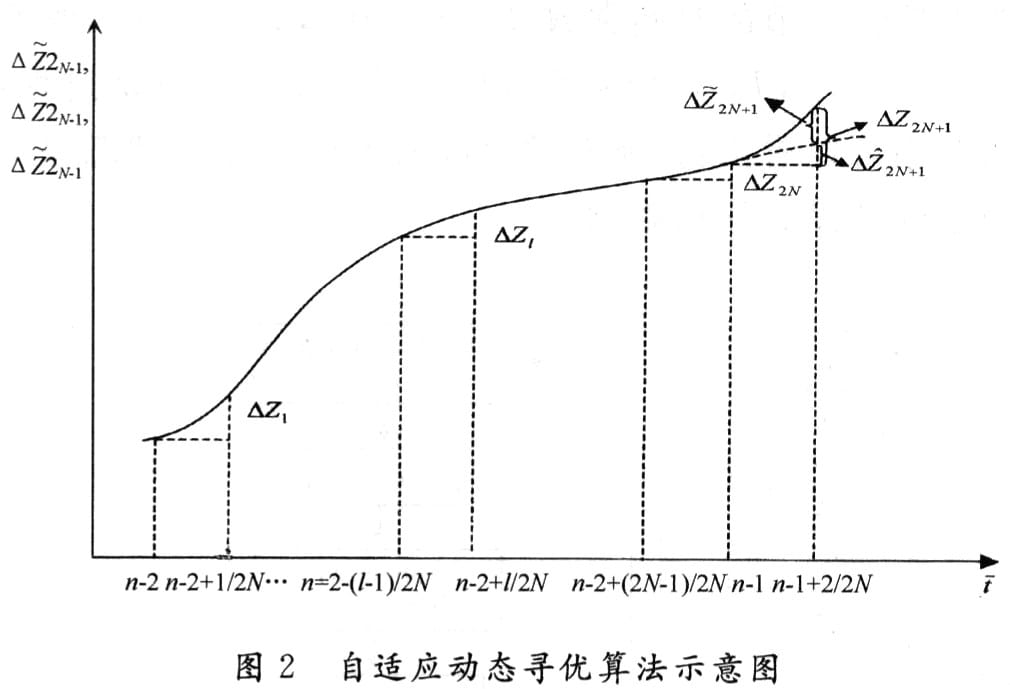
图2中:如果在t=n―l不加试探阶跃信号时,△Z2N+1系统输出的预估差值;在t=n一1加试探阶跃信号时,△Z2N+1系统输出的实际差值;在比较点上△Z2N+1是系统输出的实际差值与预估差值的比较差值即:
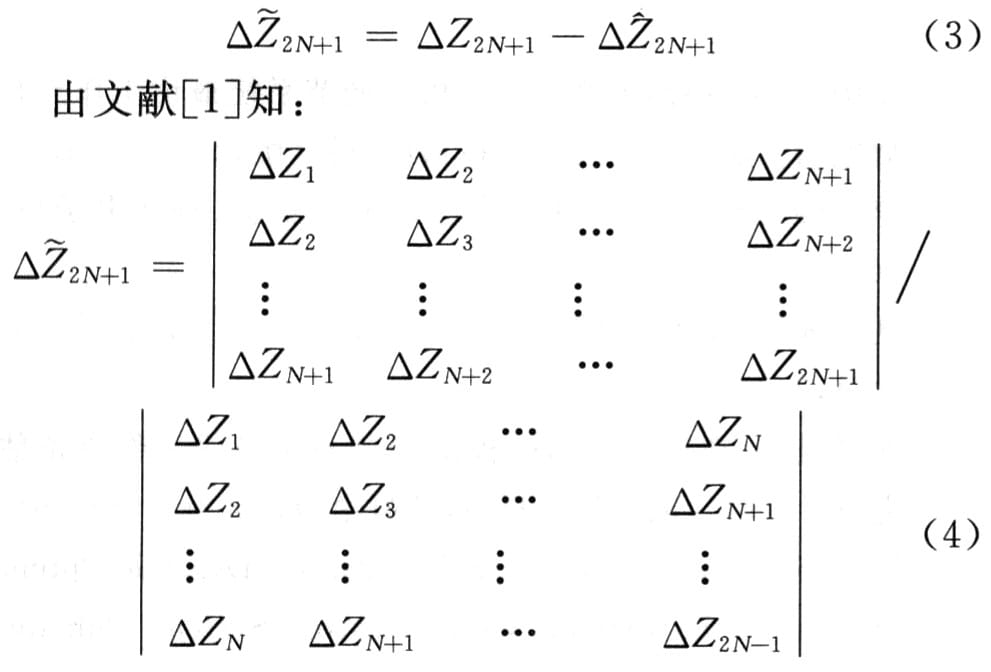
根据式(3)可知极值调节控制对象的输出采样值△Z1,△Z2,…,△Z2N+1来判断步进增量方向,步进方向的逻辑判别式为:
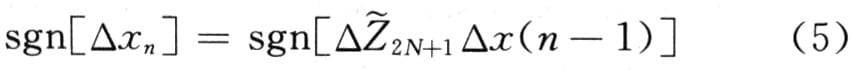
式中,sgn[△xn]指的是△x的符号。由式(4),(5)可以看出,步进方向的逻辑判别式与控制对象的惯性时间常数Tl,T2,…,TN无关。因此这些参数随时间的缓慢变化并不能影响步进方向的逻辑判别式,换言之,式(4)与式(5)能自己适应对象参数的变化,因而称作自适应为动态寻优算法。以这种算法为核心设计的极值调节控制系统,不仅能自动识别参数,还能自动适应这些参数的变化。因此只要知道极值调节控制对象线性部分的阶数就能正确地进行动态寻优,在寻优的过程中,无论控制对象线性部分的参数变化与否都不会对寻优结果的正确性有任何影响。仿真研究的结果充分证明了这一点。
2 仿真研究
对于非线性极值特性,有:
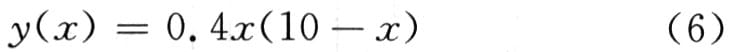
极值特性未飘移时,最初的极值点为(5,10),极值调节器由式(4)和式(5)实现。仿真程序框图如图4所示。
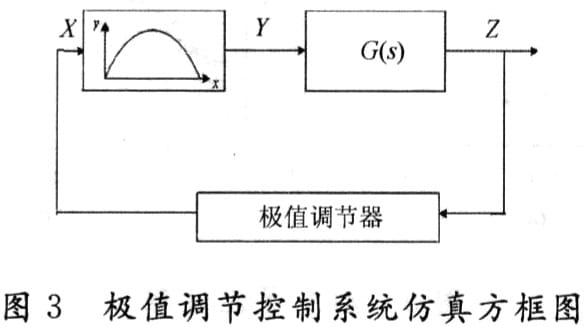
程序框图说明:初始化的主要任务是设置变量初值,输入各种参数;N阶惯性环节用四阶龙格库塔法实现;根据自适应动态寻优算法的要求,把每一步进周期分成 2N等份,采样周期△t=T0/2N,L=2N+1计算AZ2N+1,并判断步进增量方向,为下次送步进阶跃做好准备。L=2N时根据上次△Z2N+1以及△x(n一1)的符号送第n步的步进阶跃。
3 仿真结果
在实际工业生产过程中,由于要准确地辨识控制对象的参数极其困难,因此采用自适应动态寻优方法就不需要辨识控制对象的参数,而且还能自动地适应参数的飘移。只要知道控制对象线性部分的阶数就能正确地进行动态寻优。同时,受扰动的影响极值特性会缓慢的飘移,最优工作点也会随之飘移,因此控制系统的任务就是在动态过程中不断地搜寻最优工作点。所以仿真的目的就在于检验控制系统能否很好地完成上述工作任务。

